What Is A Bit?
I recently discovered that bit is actually an abbreviation for binary digit. But that does not really answer the question of what is a bit, does it? First and foremost, binary refers to a system that is composed of or involves two elements. Therefore, we can deduce that a binary digit (bit) is a digit that can contain one of two states. This is an abstract and crude interpretation but I believe it explains the concept, in words, quite well.
I like to think that a bit is analogous to an electron. Both a bit and the fundamental particle are of the smallest caliber in their respective worlds of computing and physics (let's not get into a debate about quantum computing and quarks, okay?).
An individual bit can have either a value of 1 or 0. While these two values are fixed, the information they describe can vary. For instance, a bit can represent:
- True or false
- On or off
- Positive voltage or 0 voltage
| Binary Digit (bit) | Example Representations |
|---|---|
| 0 | False, off, no voltage |
| 1 | True, on, some voltage |
Now you are thinking: "Wow David, that is awesome but what can I do with something that can only represent two states?"
Well, in essence, you can portray any binary system with a single bit. The only limitation is your imagination. And also any system that relies on more than two states.
While a lone bit sure seems suave and can tackle any twofold problem, imagine what an army of bits can accomplish.
What is a nibble?
A nibble is a set of four bits. Next section.
If only it was that simple (maybe it is). A nibble (sometimes spelled nybble) has sixteen (2^4) possible values:
| Decimal (base 10) | Binary (base 2) | Hexadecimal (base 16) |
|---|---|---|
| 0 | 0000 | 0x00 |
| 1 | 0001 | 0x01 |
| 2 | 0010 | 0x02 |
| 3 | 0011 | 0x03 |
| 4 | 0100 | 0x04 |
| 5 | 0101 | 0x05 |
| 6 | 0110 | 0x06 |
| 7 | 0111 | 0x07 |
| 8 | 1000 | 0x08 |
| 9 | 1001 | 0x09 |
| 10 | 1010 | 0x0A |
| 11 | 1011 | 0x0B |
| 12 | 1100 | 0x0C |
| 13 | 1101 | 0x0D |
| 14 | 1110 | 0x0E |
| 15 | 1111 | 0x0F |
Sir David, why does a nibble have 16 (2^4) possible values?
Short Introduction to Number Systems
We actually use the base 10 system every day without much thought because that is what we are accustomed to.
I will discuss number systems in more detail in another post but just know that you have already learned the basic idea of number systems in grade school.
Remember the concept of ones, tens, and hundreds places? That is the base 10 system!
Let's use the number 12 as an example. The digit 2 is in the ones place and the digit 1 is in the tens place. As a result, we have 2 ones and 1 tens and that adds up to 12. Professor Tran is currently accepting students, just fill out the newsletter form on the top right corner :).
Now, let's transfer that same concept to a nibble. Remember, a bit uses the base 2 system. Therefore, the nibble 0101 would equate to 1 ones, 0 twos, 1 fours, and 0 eights (right to left). Adding the aforementioned values would give us the base 10 number of 5. You can verify this by referring to the table above (please be right, I can't afford to lose my nonexistent tenure over this).
The maximum value for a nibble is 1111 and you can use the same rule to calculate that it equals the decimal number 15. As a result, a nibble can only contain one of sixteen values (0 - 15).
For the impatient or curious readers (or both), see if you can figure out a general formula for base system calculations from the previous nibble example in a vague table format:
| 2^3 | 2^2 | 2^1 | 2^0 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
This will likely require some additional research but try to apply this to a base 16 system to get the corresponding hexadecimal!
Hexadecimals are mentioned because a nibble can represent one hexadecimal digit (or vice-versa).
What is a byte?
A byte is a collection of eight bits.
A byte has 256 (2^8) possible values and can represent two hexadecimal digits.
From my limited experience and partial bias, a byte seems to be the predominant bit construct.
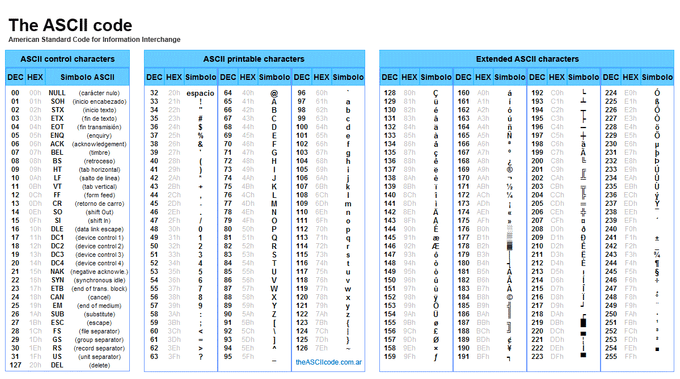
Bytes are also used for American Standard Code for Information Interchange (ASCII) encoding to provide numerical representations for numbers, English characters, and more:
As a side note, a bit is abbreviated with a lowercase b and a byte with an uppercase B. These units are prevalent in data transfers so take a closer look the next time you download something!
Closing Thoughts
There are definitely more binary constructs than the ones mentioned here but this post was not meant to be encyclopedic. I hope that this introduction inspires you to learn more about the world of bits. Another fascinating concept I recommend you explore is word (it is more interesting than it sounds, I promise).
Recall the binary joke I mentioned in my introductory post:
There are only 10 types of people in the world: Those who understand binary, and those who don’t.
I have full confidence that you now understand the meaning behind it! But I am a man of my words (when I remember) and I stated that I would explain it. 10 is binary for 2 (0 ones and 1 twos). Hopefully the explanation did not devalue the joke's humor!
Why do you think the base 10 system is so ubiquitous in our current society? Do you believe that there is a universal number system that expands beyond our known universe? If so, what type of system do you think that would be?